This note was first taken when I learnt the machine learning course on Coursera.
Lectures in this week: Lecture 8.

Neural Networks

Check [this link](https://medium.com/datathings/neural-networks-and-backpropagation-explained-in-a-simple-way-f540a3611f5e) to see the basic idea of NN and forward/backward propagation.

• Algorithms try to mimic the brain.
• 80s, 90s (very old)
• activation function = sigmoid (logistic) $g(z)$
• (sometimes) $\theta$ called weights parameters

• Neural network: first layer (input layer), intermidiate layers (hidden layer) and the last layer (output layer)

  

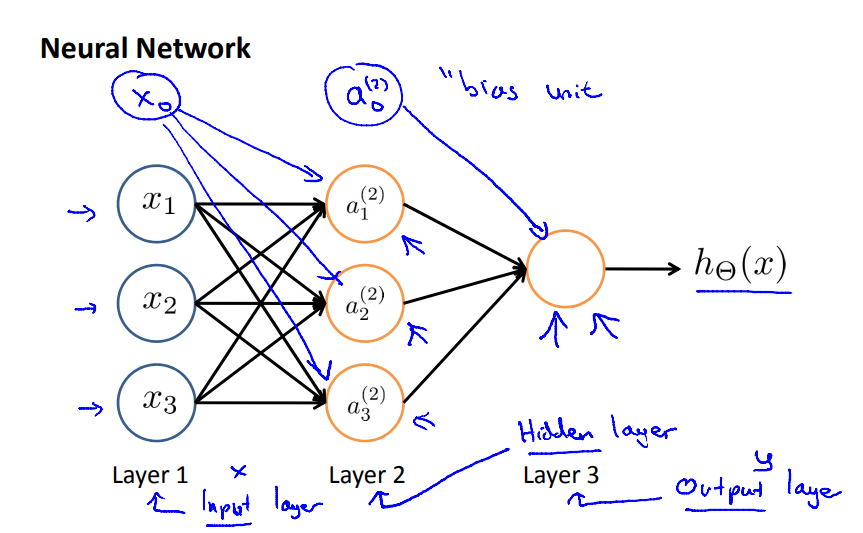
• Notations:

  • $a_i^{(j)}$ = “activation” of unit $i$ in layer $j$

    $$ a_{\text{unit}}^{(\text{layer})} $$
  • $\Theta^{(j)}$ = matrix of weights controlling function mapping from layer $j$ to layer $j+1$

  • $\Theta \in \mathbb{R}^{m\times n+1}$ where $m$ = number of unit in current layer, $n$ = number of units in previous layer (not include unit 0).

    $$ \begin{align} \Theta^{(\text{previous})} &: \text{previous layer} \to \text{current layer} \\ \Theta^{(\text{previous})} &\in \mathbb{R}^{\text{current} \times (\text{previous}+1)} \end{align} $$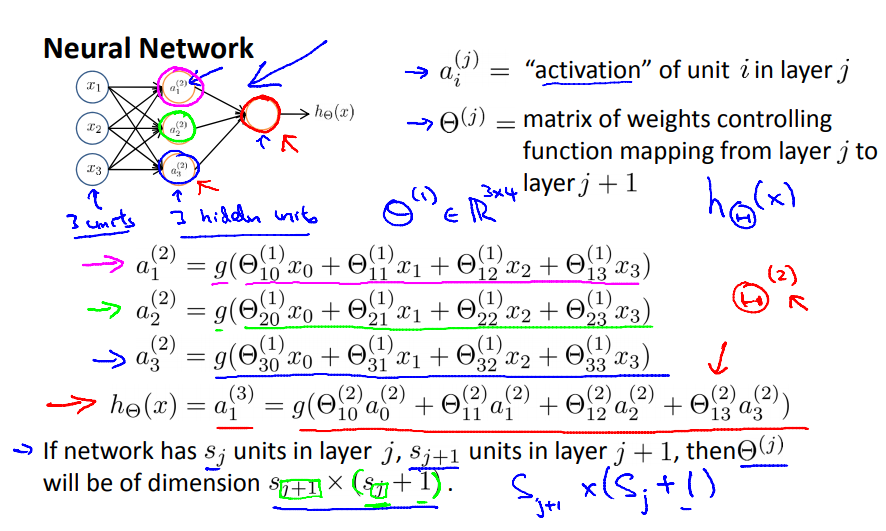

    

    $$ a_{k\in \text{current units}}^{(\text{current layer})} = g\left( \sum_{i\in \text{prev units}} \Theta_{ki}^{(\text{prev layer})} a_i^{(\text{prev layer})} \right) $$

Forward propagation: vectorized implementation

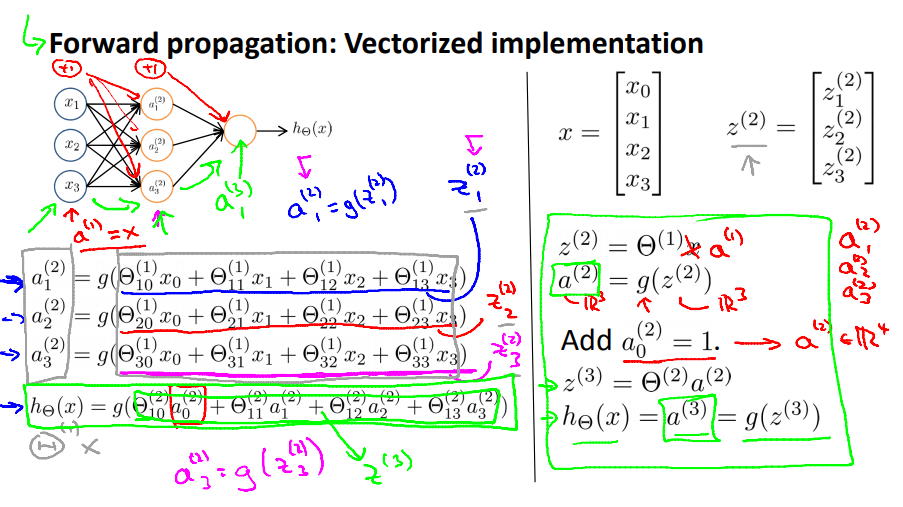
• Neural network is look like logistic regression, except that instead of using $x_1, x_2, \ldots$, it’s using $a^{(j)}_1, a^{(j)}_2, \ldots$
• Neural network learning its own features.
• Architectures = how different neurons connected to each other.

• Final

  $$ \begin{align} h_{\theta}(x) = a^{(j+1)} = g(z^{(j+1)}) = g(\Theta^{(j)}a^{(j)}). \end{align} $$

Examples and Intuitions I

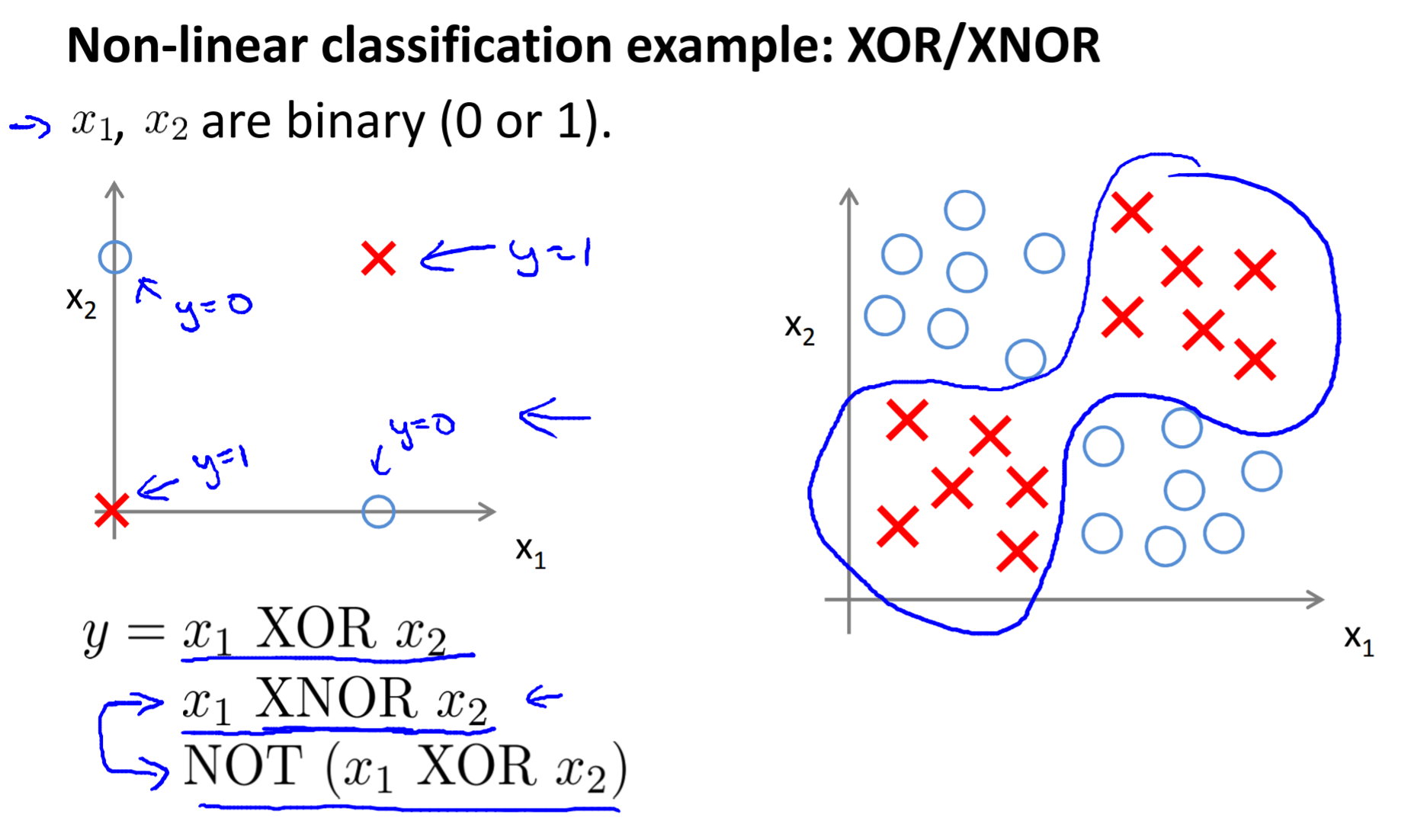
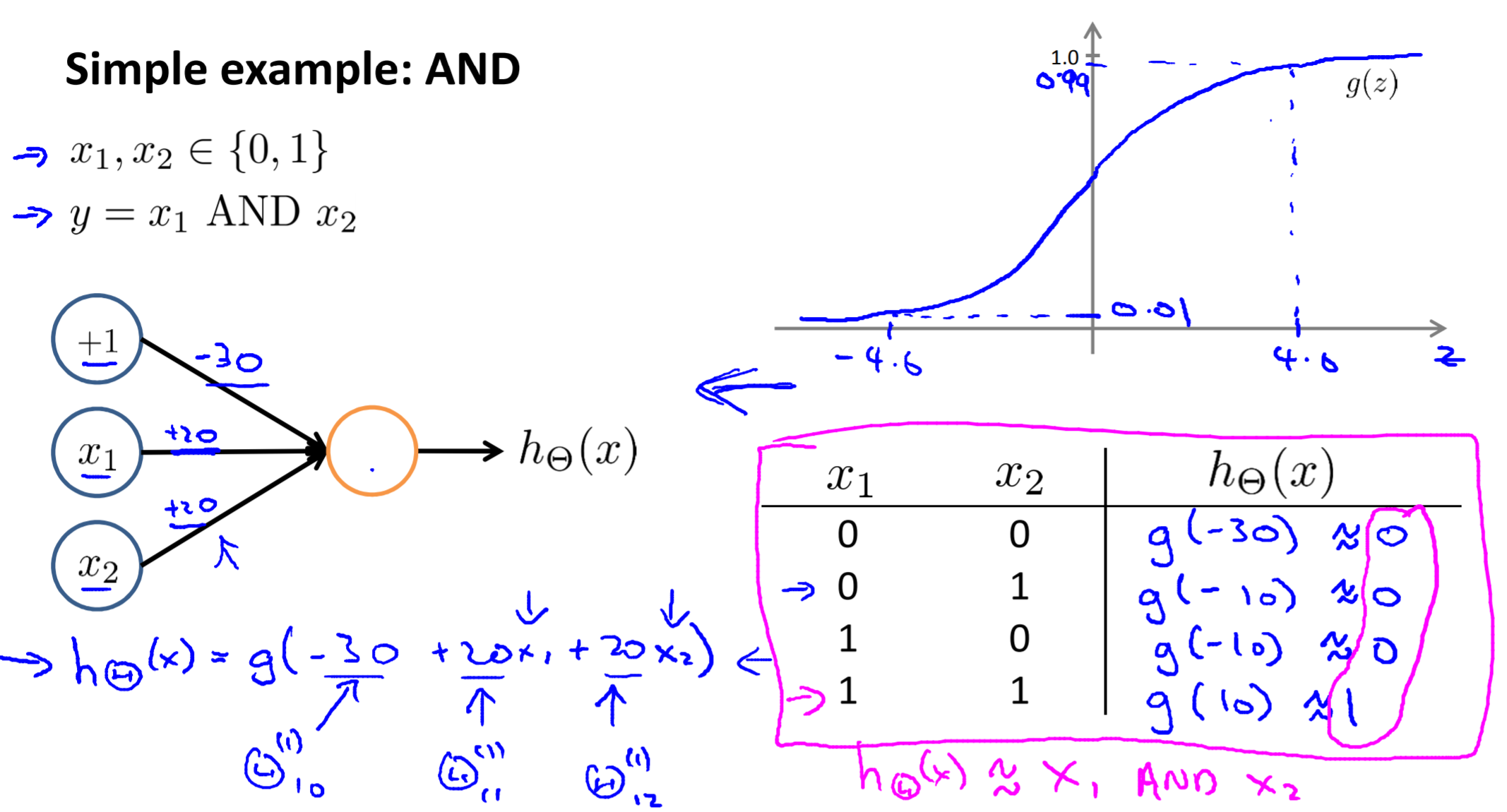
Examples and Intuitions II

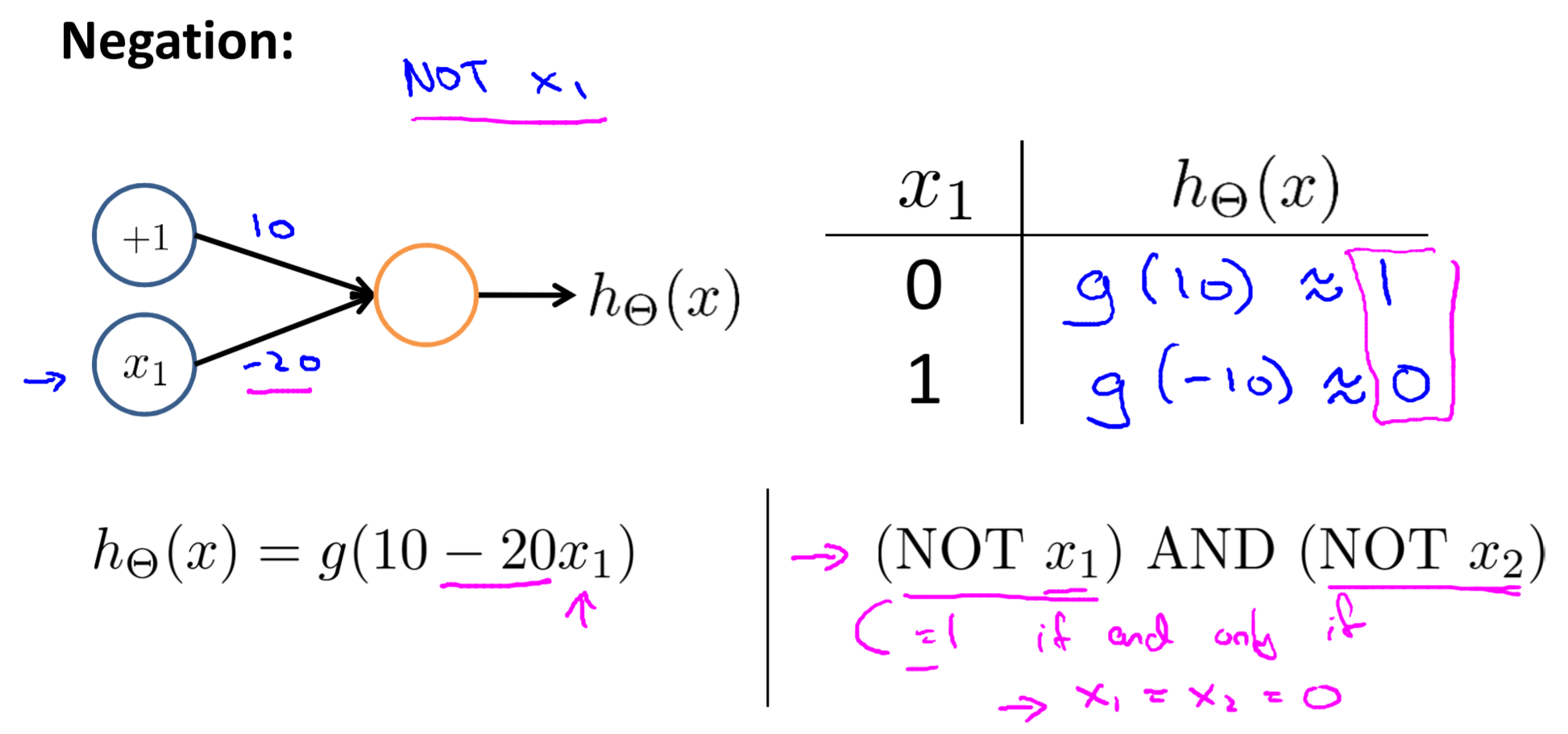
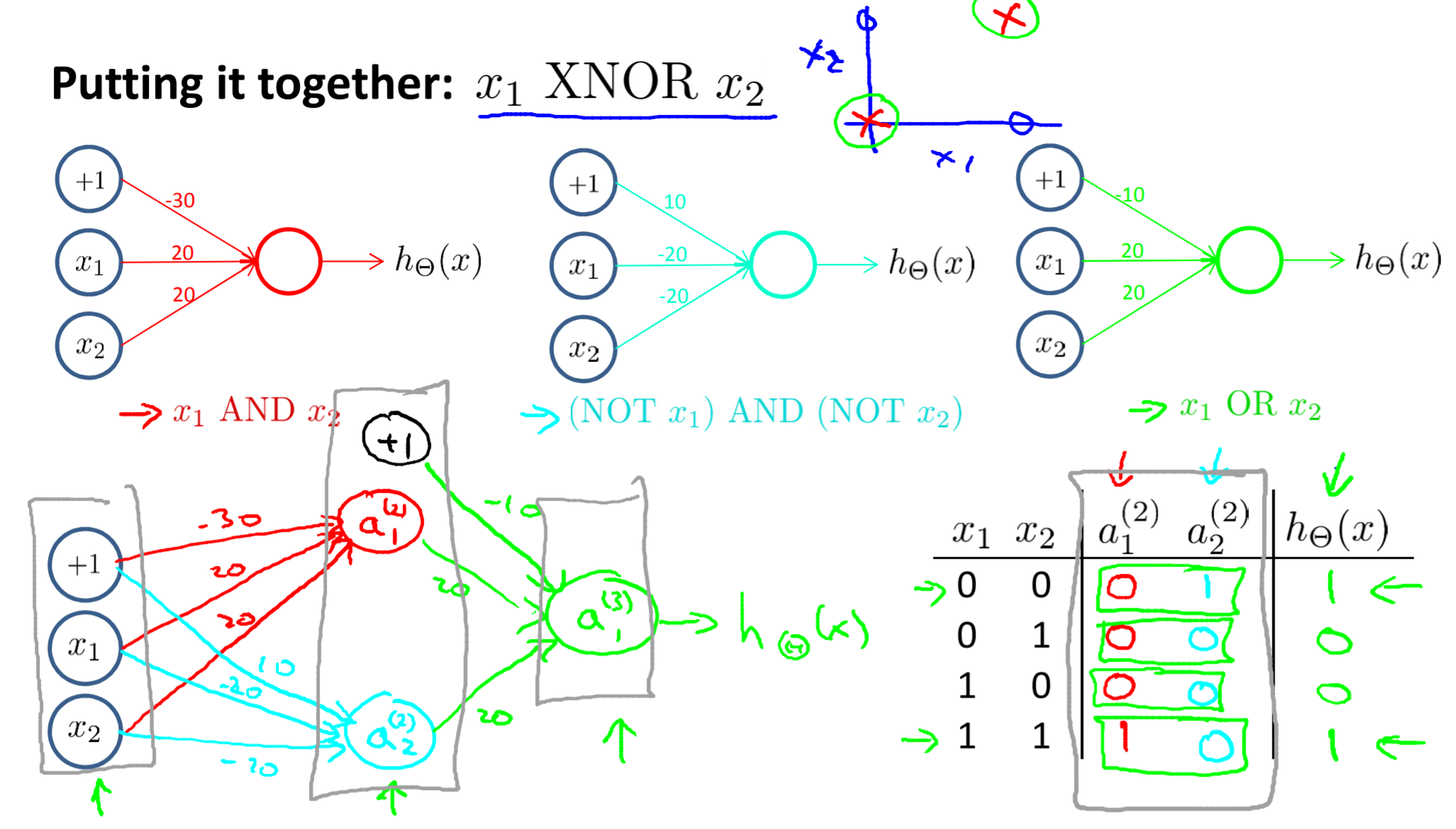
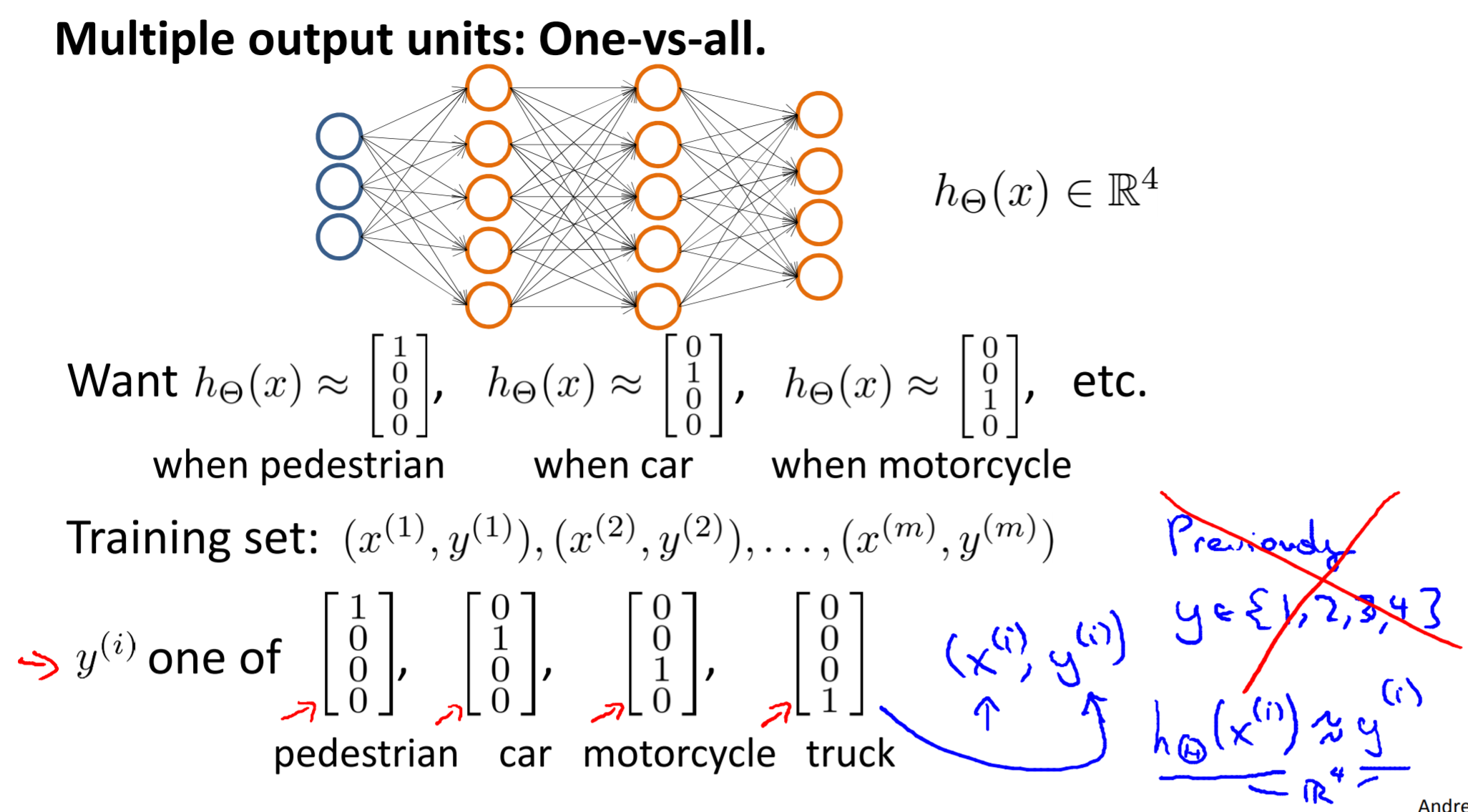
Multiclass classification

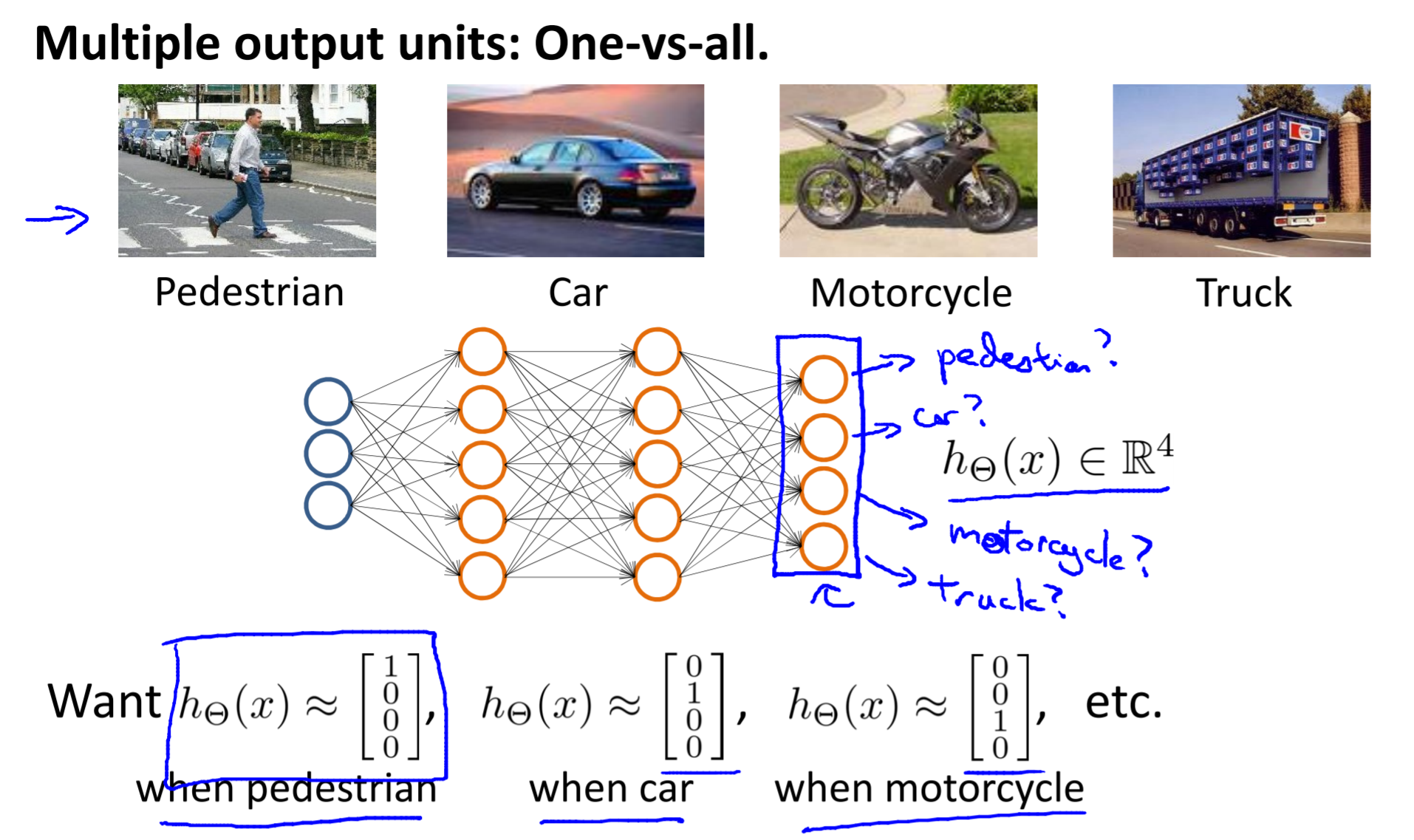
Exercise Programmation: Multi-class Classification and Neural Networks

• lrCostFunction.m

  This ex is the same with the one in the previous week.

  h = sigmoid(X*theta); % hypothesis
  J = 1/m * ( -y' * log(h) - (1-y)' * log(1-h) ) + lambda/(2*m) * sum(theta(2:end).^2);
    
  grad(1,1) = 1/m * X(:,1)' * (h-y);
  grad(2:end,1) = 1/m * X(:,2:end)' * (h-y) + lambda/m * theta(2:end,1);
  

• oneVsAll.m

  initial_theta = zeros(n + 1, 1);
  options = optimset('GradObj', 'on', 'MaxIter', 50);
  for c = 1:num_labels
  	  [theta] = fmincg (@(t)(lrCostFunction(t, X, (y == c), lambda)), initial_theta, options);
  	  all_theta(c,:) = theta(:);
  end
  

  info fmincg works similarly to fminunc, but is more more efficient for dealing with a large number of parameters.

• predictOneVsAll.m

  h = X * all_theta';
  [~, p] = max(h,[],2);
  

• predict.m : “you implemented multi-class logistic regression to recognize handwritten digits. However, logistic regression cannot form more complex hypotheses as it is only a linear classifier.”

    X = [ones(m, 1) X]; % add column 1 to a2
    z2 = X * Theta1';
    a2 = sigmoid(z2);
    a2 = [ones(m, 1) a2]; % add column 1 to a2
    h = a2 * Theta2';
    [~, p] = max(h,[],2);