Xem các phần khác tại đây.

Linh tinh

Tại sao gọi là “Energy norm”? : Thỉnh thoảng norm sau đây được gọi là Energy norm, tại sao?

$$\lVert u \rVert_{1, 2}^2=\int_{\Omega} \lvert u(x)\rvert^2\, dx + \int_{\Omega} \lvert \nabla u(x)\rvert^2\, dx$$

Có giải thích ở đây nhưng mà không hiểu lắm.

Harmonic function

Harmonic function: In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function $f:U \to R$ ($U$ is open subset of $\mathbb{R}^n$) which satisfies Laplace’s equation, i.e. $\Delta f=0$ everywhere on $U$. Cái này là đủ để định nghĩa harmonic function rồi.

---

Harmonic functions (see Figure dưới) are the classical example to which the strong maximum principle applies. Formally, if $f$ is a harmonic function, then $f$ cannot exhibit a true local maximum within the domain of definition of $f$. In other words, either $f$ is a constant function, or, for any point $x_0$ inside the domain of $f$, there exist other points arbitrarily close to $x_0$ at which $f$ takes larger values.

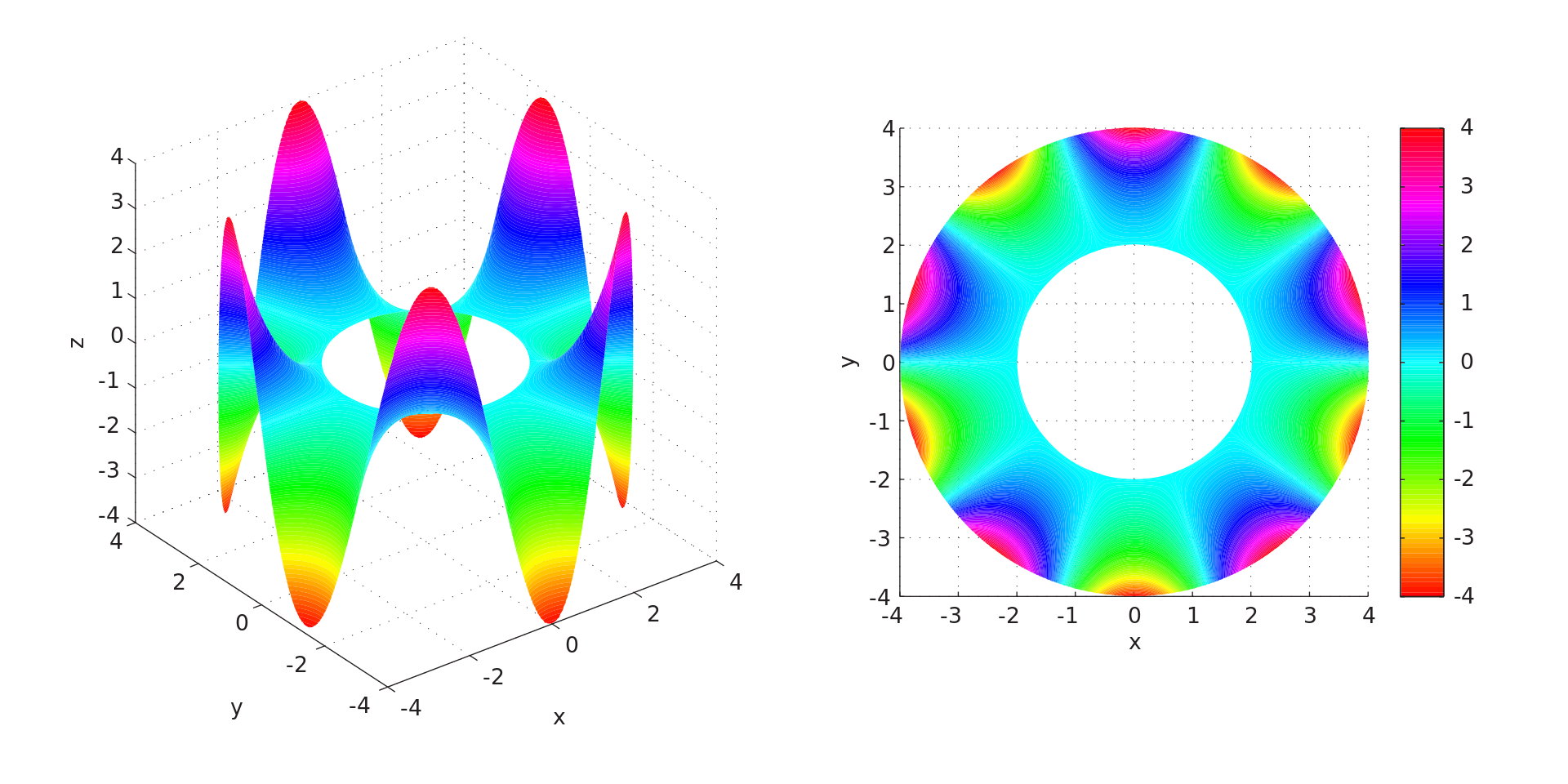
Let f be an harmonic function defined on some connected open subset $D$ of the Euclidean space $\mathbb{R}^n$. If $ x_0$ is a point in $D$ such that $f(x_0)\ge f(x)$ for all $x$ in a neighborhood of $x_0$, then the function $f$ is constant on $D$.

Có thể thấy trong hình trên giá trị cao nhất của hàm số chỉ đạt được trên biên.

By replacing “maximum” with “minimum” and “larger” with “smaller”, one obtains the minimum principle for harmonic functions.

Landau symbol 0 (big 0)

[link to pdf file, page 4] The Landau symbol O, sometimes referred to as “big Oh”, is used to compare the behavior of one function $f(h)$ with another function $g(h)$ as $h \to 0$. One writes

$$\begin{align*} f(h)=O(g(h)) \text{ if } \vert f(h)\vert \le C\vert g(h)\vert , C>0. \end{align*}$$

for all $h$ sufficiently small such that $\lim_{h\to 0}\frac{\vert f(h)\vert}{\vert g(h)\vert }\le C< \infty$.

For example, consider a Taylor series expansion for $\sin(x)$. One can write

$$\sin x= x-\dfrac{x^3}{3!}+O(x^5)$$

since

$$\lim_{x\to 0}\dfrac{\sin x-x-\frac{x^3}{3!}}{x^5}=\dfrac{1}{5!} = \text{constant}.$$

The trace

Trong đại số tuyến tính thì vếch của ma trận vuông (the trace of a square matrix) là tổng của cá hệ số trên đường chéo chính.

Nhưng cái cần biết ở đây là, nếu $u:\Omega \to \mathbb{R}$, thì khi ấy trace của $u$ là gì? Khi xem trên Wiki về Trace operator, có thể hiển nôm na nó liên quan đến các vấn đề về tồn tại nghiệm trên biên. Tồn tại trace tức tồn tại giá trị trên biên (check lại xem chính xác không).

Nếu $u\in H^1_0(\Omega)$ thì có thể hiểu là $u\in H^1(\Omega)$ với trace trên biên $\partial \Omega$ bằng $0$.

---

Trace theorem : $\Vert{u}\Vert_{L^2(\partial\Omega)}\le C\Vert{u}\Vert_{H^1(\Omega)}$, từ đây cũng có thể suy ra $\Vert u\Vert_{L^2(\partial\Omega)}\le C\Vert \nabla u\Vert_{L^2(\Omega)}$.

Normal derivative

Cập nhật ngày 17-02-2015 : Thật ra cái normal derivative này cứ áp dụng theo định nghĩa là được. Định nghĩa của nó chính là đạo hàm theo hướng của cái normal vector, tức là $\nabla f\cdot \mathbf{n}$. Trong đó

$$\nabla f = (\partial_x f,\partial_y f,\partial_z f)$$

còn $\mathbf{n} = (n_x,n_y,n_z)$ chính là normal derivative với $\Vert\mathbf{n}\Vert=1$. Quan trọng ở đây là ta cần xác định $\mathbf{n}$ trong từng trường hợp là cái gì. Nếu xét trên mặt phẳng song song với $Oyz$ (tức vuông góc với $Ox$) thì khi ấy vector pháp tuyến sẽ song song với $Ox$, hay nói cách khác, $\mathbf{n} = (1,0,0)$. Suy ra $\nabla f\cdot \mathbf{n} = \partial_x f$.

A normal derivative is a directional derivative taken in the direction normal (that is, orthogonal) to some surface in space.

$$\frac{ \partial f}{\partial n} = \nabla f({x}) \cdot \mathbf{n} = \nabla_{\mathbf{n}}{f}({x}) = \frac{\partial f}{\partial {x}}\cdot\mathbf{n} = Df({x})[\mathbf{n}]$$ $$\frac{\partial }{\partial \mathbf{n}}= e_{x}\frac{\partial }{\partial x}+e_{y}\frac{\partial }{\partial y}+e_{z}\frac{\partial }{\partial z}$$

where $e_x, e_y, e_z$ are the components of the surface normal vector $\mathbf{n}=e_x\mathbf{i} + e_y\mathbf{j} + e_z\mathbf{k}$, $\Vert\mathbf{n}\Vert=1$.

An example, the surface is parallel to the $yz$ plane and facing to $x$, then $e_x=1, e_y=0, e_z=0$. So

$$\dfrac{\partial}{\partial \mathbf{n}} = \dfrac{\partial}{\partial x}$$

Ghi nhớ : Nếu có song song với trục toạ độ/mặt phẳng toạ độ thì “cắt cái gì sẽ đạo hàm theo cái đó”.

outward normal vector là gì?

Norms

Norm in H1/2 (H^(1/2)) $H^{1/2}$ : Let $\Omega\subset \mathbb{R}^d$ a Lipschitz domain and $\Gamma:=\partial\Omega$. For $u\in \mathcal{C}^{\infty}$, we define (cái này lấy từ đây)

$$\Vert u\Vert_{H^{1/2}(\Gamma)} = \inf_{v\in H^1(\Omega),v\vert_{\Gamma}=u}\Vert v\Vert_{H^1(\Omega)}$$

$g_0\in H^{1/2}(\Gamma)$ means that there exists at least a function $u_0\in H^1(\Omega)$ such that $u_0=g_0$ on $\Gamma$.

---

Còn cái $\Vert u \Vert_{H^{1/2}(\Omega)}$ with $\Omega$ open thì sao? (Cái này thằng Oussama cùng phòng hỏi)

Xem ở đây có thể có gợi ý chút chút nhưng trong cái này $\Omega’ \subset \mathbb{R}^{n-1}$.

Ở note này (section 4.) và note này (mục 2.3), ông tác giả định nghĩa $H^s(\mathbb{R}^n), s\in \mathbb{R}$ luôn nhưng cái này là định nghĩa trên $\mathbb{R}^n$ thông qua khai triển Fourier của $u$ (là $\hat{u}$) trong khi cho $\mathbb{\Omega}$ mở trong $\mathbb{R}^n$ thì không có cái Fourier này (cái này Osama nói, chưa kiểm chứng lại được). Nói chung là khác nhau.

Fourier transform $\hat{u}$ of a function $u\in C_0^{\infty}(\mathbb{R}^n)$,

$$\hat{u}(\xi) = (\dfrac{1}{2\pi})^{d/2}\int_{\mathbb{R}^n}exp(-i\xi\cdot x)u(x)dx$$

Ở note này (mục 2.3), cũng có định nghĩa cho $\Omega \subset \mathbb{R}^n$ Lipchitz domain. Note này của Ronald H.W. Hoppe.

Test functions - Dirichlet BC - Neumann BC

Tôi có một thắc mắc: Khi nào thì test function nằm trong $V_0$, còn khi nào thì chỉ nằm trong $V$ thôi?. Đọc bài viết này làm cho tôi hiểu thêm được vài phần.

Chú ý : có thể xem thêm câu trả lời của Shuhao Cao trên StackExchange.

Ví dụ ta xét strong form of Poisson equation

$$\begin{align*} \begin{cases} \Delta T&=f(x), x\in \Omega\\ T&=u(x), x \in \Gamma_D\\ \nabla T\cdot \mathbf{n} &= g(x), x\in \Gamma_N \end{cases} \end{align*}$$

where $\Omega \subset \mathbb{R}$. $\Gamma_D$ is the part of the boundary where Dirichlet boundary conditions are given, $\Gamma_N$ is the part of the boundary where Neumann boundary conditions are given. The weak form is

$$\int\limits_{\Omega} \nabla T \cdot \nabla s \, \mathrm{d}\Omega = \int\limits_{\Gamma_D} s \cdot (\nabla T \cdot \mathbf{n}) \, \mathrm{d}\Gamma + \int\limits_{\Gamma_N} s \cdot (\nabla T \cdot \mathbf{n}) \, \mathrm{d}\Gamma - \int\limits_{\Omega} f \cdot s \, \mathrm{d}\Omega.$$

Chúng ta cần lưu ý hai điểm đối với Dirichlet condition : một cái là điều kiện $T=u(x)$ thì vẫn sử dụng như ý nghĩa của nó. Một cái là cái tích phân $\int_{\Gamma_D}$. To be consistent we have to use only the Dirichlet conditions and avoid the integral term. Đó là lý do vì sao ta sử dụng test function $s\in V_0$

That is why Dirichlet conditions in FEM terminology are called Essential Boundary Conditions. These conditions are not a part of the weak form and they are used as they are.

Còn Neumann BC thì có thể áp dụng được trong weak form.

Wellposed problem

Wellposed problem (wikipedia) : The mathematical term well-posed problem stems from a definition given by Jacques Hadamard. He believed that mathematical models of physical phenomena should have the properties that

• A solution exists
• The solution is unique
• The solution’s behavior changes continuously with the initial conditions.

Trong ErnDiscont trang 20 pdf có nói về định lý Banach-Necas-Babuska về wellposed problem, bao gồm 2 ý:

• Inf-sup stability, cái điều kiện này cũng có thể được ghi dưới dạng

$$\exists C>0:\forall x\in X: C\Vert{v}\Vert_{X}\le \sup_{w\in Y\backslash\{0\}}\dfrac{a(v,w)}{\Vert{w}\Vert_{Y}}$$ $$\inf_{v_h\in V}\sup_{w_h\in V}\dfrac{a_h(v_h,w_h)}{\Vert{v_h}\Vert_{A}\Vert{w_h}\Vert_{A}}\ge C$$

• For all $w\in Y$ : $( \forall v\in V, a(v,w)=0 ) \Rightarrow (w=0).$

Convergence

Pointwise convergence : (hội tụ điểm). For each $x\in D$, for all $\varepsilon > 0, \exists N>0, \forall n\ge N, \vert f_n(x)-f\vert < \varepsilon$.

Uniformly convergence (hội tụ đều). For all $\varepsilon > 0, \exists N>0, \forall n\ge N, \vert f_n(x)-f\vert < \varepsilon$ for all $x\in D$.

Uniformly convergence $\Rightarrow$ pointwise convergence but ngược lại thì không đúng.

---

Monotone convergence theore (cf. wiki)

• If a sequence of real numbers is increasing and bounded above, then its supremum is the limit.
• If a sequence of real numbers is decreasing and bounded below, then its infimum is the limit.

Lesbegue’s monotone convergence theorem (cf. Rudin, p.21) Let ${f_n}$ be a sequence of measurable functions on $X$, and suppose that

1. $0<f_1(x)<f_2(x)<\ldots<\infty$, for every $x\in X$,
2. $f_n(x)\to f(x)$ as $n\to \infty$, for every $x\in X$.

then $f$ measurable and $\int_X{f_nd\mu}\to \int_X{fd\mu}$ as $n\to \infty$.

---

Lebesgue’s Dominated Convergence Theorem (cf. wiki, Rudin, p.26 )

Suppose ${f_m}$ is a sequence of real measurable functions on $E$ such that there is a real function $f$ and an integrable real function $g$ on $E$ having the following propreties

1. $f(x) = \lim_{m\to \infty}f_m(x), \quad \forall x\in E$
2. $\vert f_m(x)\vert \le g(x), \quad \forall x\in E, m=1,2,\ldots$

Then $f$ is integrabole on $E$ ($f\in L^1(E)$),

$$\lim_{m\to\infty}\int_Ef_m \,dx= \int_E(\lim_{m\to\infty}f_m)\,dx$$

---

Weak/weak* convergence là gì?

• Strong convergence : $x_n,x\in X: x_n \mapsto x \Leftrightarrow \lim_{n\to \infty}\Vert{x_n-x}\Vert=0$

• Weak convergence : $x_n,x\in X: x_n \overset{w}{\rightarrow} x \Leftrightarrow \forall \mu \in X^\ast : \lim_{n\to \infty}\left<{x_n,\mu}\right> = \left<{x,\mu}\right>$

• Weak* (weak star) convergence : $x_n,x\in X^\ast: x_n \overset{w^\ast}{\rightarrow} x \Leftrightarrow \forall \mu \in X : \lim_{n\to \infty}\left<{\mu,x_n}\right> = \left<{\mu,x}\right>$

Weak convergence propertiess

• Every bounded sequence in $H^1_0(\Omega)$ has a subsequence that converges weakly in $H^1_0(\Omega)$ because $H^1_0(\Omega)$ is a reflexive Banach space and based on the weak compactness. Xem thêm ở một câu hỏi trên stackexchange và chứng minh ở đây.
• Every bounded sequence in a reflexive Banach space $X$ (e.g., when $X$ is a Hilbert space) has a weakly convergent subsequence. $\Leftarrow$ Cái này có thể chứng minh bằng cách áp dụng định lý Banach-Alaoglu Theorem.
• Since every closed and bounded set is weakly relatively compact (its closure in the weak topology is compact), every bounded sequence $x_n$ in a Hilbert space $H$ contains a weakly convergent subsequence. Wiki.

$\Rightarrow$ 3 cái trên có thể hiểu nhanh gọn : Mỗi bounded sequence in a relexive Banach space (Hilbert space) has a weakly convergent subsequence. Mà $H^1_0$ cũng là Hilbert space.

• A weakly convergent sequence in a Hilbert space $H$ is bounded. Xem chứng minh ở Theorem 3.3.15 sách của Debnath2005

• The norm is (sequentially) weakly lower-semicontinuous: if $x_{n}$ converges weakly to $x$, then $\Vert x\Vert \leq \liminf_{n\to \infty}\Vert x_{n}\Vert,$ and this inequality is strict whenever the convergence is not strong. For example, infinite orthonormal sequences converge weakly to zero, as demonstrated below.

  $$0 \le \Vert{x_n-x}\Vert^2 = \Vert{x}\Vert^2 - 2Re\langle{x_n,x}\rangle + \Vert{x}\Vert^2.$$

  By hypothesis, $\langle{x_n,x}\rangle \to \langle x,x\rangle=\Vert{x}\Vert^2$. So taking the $\lim\inf$ above,

  $$0 \le \Vert{x}\Vert^2 - 2\Vert{x}\Vert^2 + \lim\inf\Vert{x_n}\Vert^2.$$

• (nói thêm + rõ hơn cái ở trên) If $x_n \rightharpoonup x$ then $\langle x_n,x\rangle \to \langle x,x\rangle=\Vert x\Vert^2$, but $\vert\langle x_n,x\rangle\vert \le \Vert x_n\Vert \Vert x\Vert$ , this implies $\lim\inf\Vert x_n\Vert \ge \Vert x\Vert$.

• If $x_{n}$ converges weakly to $x$ and we have the additional assumption that $\lVert x_{n}\rVert \to \lVert x\rVert$ , then $x_{n}$ converges to $x$ strongly:

  $$\displaystyle \langle x-x_{n},x-x_{n}\rangle =\langle x,x\rangle +\langle x_{n},x_{n}\rangle -\langle x_{n},x\rangle -\langle x,x_{n}\rangle \rightarrow 0.$$

• If $\dim X<\infty$ then weak convergence implies strong convergence. Xem chứng minh ở đây.

• If the Hilbert space is finite-dimensional, i.e. a Euclidean space, then the concepts of weak convergence and strong convergence are the same.

• If ${x_n}$ bounded in $H^1$, there exists a subsequence that convergences weakly in $H^1$, and because $H^1 \hookrightarrow L^2$ nên $x_n$ converges strongly in $L^2$. Có một chứng minh trên stackexchange mà quên.

• $L^2(\Omega)$ is a Hilbert space. Xem chứng minh ở wolfram

  Nói thêm : Hilbert space là một reflexive Banach space, nó có vài tính chất như “Mỗi bounded sequence in a relexive Banach space (Hilbert space) has a weakly convergent subsequence. Mà $H^1_0$ cũng là Hilbert space “

• If $f_n \rightharpoonup f$ in $L^p(\Omega)$ then $f_n$ is bounded in $L^p(\Omega)$.

---

Convergence in $L^p$ ($\Vert f_n-f \Vert_{L^p(\mathbb{R})} \to 0$ ) implies subsequence converges almost everywhere. Xem thêm phản ví dụ và giải thích ở đây.

Gateaux differentials and Frechet derivatives

The Frechet derivative is defined on Banach spaces and the Gateaux derivative is a generalization of the directional derivative studied extensively in several variables.

A function defined between normed spaces differentiable in the sense of Frechet then it is Gateaux differentiable, the reciprocal is not true in general.

The Gateaux differential generalizes the idea of a directional derivative. Let $f: V\to U$ be a function and let $h\neq 0$ and $x$ be vectors in $V$. The Gateaux differential $d_hf$ is defined as

$$d_hf=\lim_{\varepsilon \to 0}\dfrac{f(x+\varepsilon h)-f(x)}{\varepsilon}$$

If the limit exists for all $h \in V$, then one says that $f$ is Gâteaux differentiable at $x$.

Cái Gateaux này giống cái đạo hàm theo hướng nhưng là bản mở rộng hơn. Cái đạo hàm theo hướng (directional derivative) là của một scalar function $f(x)=f(x_1,x_2,\ldots,x_n)$ along a vector $v=(v_1,v_2,\ldots,v_n$. Còn cái Gateaux là mở rộng sang topology vector space với several variables.

Gateaux differential có thể là một non-linear nhưng Frechet phải là một linear.

---

The Fréchet derivative is a derivative defined on Banach spaces. Let $V,W$ be Banach space and $U \subset V$ open. $f: U\to W$ is called Fréchet differentiable at $x\in U$ if there exists a bounded linear operator $Df: V\to W$ such that,

$$\lim_{h \to 0} \frac{ \Vert f(x + h) - f(x) - (Df)h \Vert_{W} }{ \Vert h\Vert_{V} } = 0.$$

Or we can write, $\frac{1}{2}$

$$f(x+h) = f(x) + (Df)h + o(\left\Vert h\right\Vert)$$

where $\lim_{h\to 0}\dfrac{o(\left\Vert h\right\Vert)}{h}=0$.

Theo như trong freefem++ doc, thì có thể ghi dưới dạng

$$F(u+\delta) = F(u) + DF(u,\delta) + o(\left\Vert \delta \right\Vert)$$

An example Gateaux but not Frechet $f(x)=\vert x\vert $. The Gateaux differential at $x=0$ is $d_hf=\lim_{\varepsilon\to 0}\frac{\vert\varepsilon h\vert}{\varepsilon}=\vert h\vert$. This is not a linear function of $h$. Therefore, the Frechet derivative doesn’t exsit.

Tìm Frechet $DF(u,\delta)$ : take $F(u+\delta)-F(u)$, sau đó isolate a term that is linear in $\delta$ rồi áp dụng định nghĩa trên để chứng minh nó là Frechet differential. Nói chung cứ xoay quanh định nghĩa mà làm.

---

If Frechet then Gateaux : xem chứng minh ở đây.

---

Newton’s method uses the Frechet derivative to replace a nonlinear problem by a sequence of linear problems (cf. this book).

Green and Stokes theorem

Wikipedia for Green’s theorem : https://en.wikipedia.org/wiki/Green’s_theorem For Stokes : here

Other links :

• The idea behind Green’s theorem (math insight)
• the fundamental theorems of vector calculus
• Using Green theorem to find area (math insight)
• green theorem examples (math insight)
• Paul’s online math notes - green theorem with example exercises

Let C be a positively oriented, piecewise smooth, simple closed curve in a plane, and let D be the region bounded by C. If L and M are functions of (x, y) defined on an open region containing D and have continuous partial derivatives there, then

$$\oint _{C}(L\,dx+M\,dy)=\iint _{D}\left({\frac {\partial M}{\partial x}}-{\frac {\partial L}{\partial y}}\right)\,dx\,dy$$

Xem các phần khác tại đây.